INTRODUCCIÓN

El estudio del rendimiento académico ha sido una preocupación constante en la investigación educativa. A nivel internacional, cada año se publican gran cantidad de artículos e informes de investigación en relación con este tema. Revistas como American Educational Research Journal y Educational Researcher de la Asociación Americana de Investigación Educativa publican regularmente resultados de investigaciones que tratan de explicar el desempeño escolar en educación primaria, secundaria y superior.
La revisión de la literatura sobre rendimiento académico ha aportado una conclusión importante y es que nos enfrentamos a un constructo de naturaleza multidimensional (Vargas y Montero, 2016) que precisa de un abordaje metodológico que permita identificar de manera integrada las variables que afectan al desempeño del estudiante; en este sentido, ha habido un cambio de enfoque en el que han ido cobrando protagonismo las investigaciones basadas en modelos predictivos. Sin lugar a dudas la comunidad científica internacional coindice en que la regresión lineal y logística son mecanismos estadísticos eficaces y viables para predecir el rendimiento académico (Choi & Hwang, 2017).
Este tipo de investigación es clave para que se puedan introducir cambios, a nivel institucional o programático, tales como tamaño de los grupos, uso de materiales didácticos o estrategias pedagógicas que produzcan, efectivamente, los impactos deseados. Diversas investigaciones (Treviño et al., 2017; Barker, 2014; Marschark, 2015; Mediavilla & Gallego, 2016; Vergel-Ortega et al., 2016) abundan en el estudio de las causas que influyen en el rendimiento académico, determinando las variables que en contextos determinados predicen su comportamiento.
En este sentido, el trabajo realizado por Treviño et al., (2017) concluye que variables como el género, la satisfacción con la titulación, simultanear estudios y trabajo a la vez y los estudios realizados previamente resultan determinantes. Este último aspecto es coincidente con otras investigaciones que incluyen además variables tales como la puntuación para el ingreso a la universidad, la condición étnica, la asistencia a una escuela pública y las habilidades psicopedagógicas (Yarnel & Bohrnstedt, 2017). Factores sociales como la educación de los padres, la provincia de procedencia y la motivación hacia el estudio fueron analizados por otras investigaciones destacando el uso de modelos estadísticos (Chaparro et al., 2015; Palomar & Estrada, 2016; Saw et al., 2017).
De igual manera diversas variables motivacionales predicen el rendimiento académico en la propuesta científica de investigadores que destacan además como factor predictivo la conducta de los estudiantes (Castellanos et al., 2017; Flores-Hernández, Sánchez-Mendiola & Martínez-González, 2016; González & Valenzuela, 2016). En los trabajos realizados por Garbanzo (2014), Gil, (2017) y Pokropek et al., (2017) las variables socioeconómicas son productoras del rendimiento académico
Respecto a la variable, prueba de ingreso a la educación superior, los hallazgos fueron coincidentes con otros resultados en la medida que el rendimiento de los alumnos estaba asociado a una puntuación alta de ingreso a la universidad (Mora, 2015). Este estudio también concluyó que el rendimiento académico de los años posteriores estaba asociado a las calificaciones obtenidas en el primer año.
Especial interés prestan diversos autores a la relación existente entre el rendimiento en la universidad y las pruebas de ingreso de matemática, como examen que mide el desarrollo lógico y algorítmico necesarios para enfrentar estudios superiores (Soria-Barreto & Zúñiga-Jara, 2014). El rendimiento académico en matemáticas es además determinado por disímiles autores a partir de un grupo de factores actitudinales, sociales, cognitivos y motivacionales (Reimann et al., 2013; Presentacion et al., 2015; Pinxten et al., 2014). Otras investigaciones se han centrado en determinar el efecto que tiene sobre el rendimiento académico las horas que el estudiante dedica al trabajo como actividad complementaria al estudio, además de diversas variables motivacionales (Katsikas & Panagiotidis, 2010; Stinebrickner & Stinebrickner, 2003).
Las investigaciones sobre rendimiento académico en los que se han utilizado técnicas como la regresión lineal o múltiple (Hamsa, Indiradevi & Kizhakkethottam, 2016), avalan la potencialidad que tienen para identificar las variables que afectan al desempeño del estudiante abriendo el abanico a otro tipo de variables no identificadas previamente como la influencia que tiene en el rendimiento académico los patrones de evaluación de los profesores (Broc, 2016)  o variables relacionadas con la indisciplina instruccional y convencional (Gotzens et al., 2015).
En síntesis, la investigación actual aporta un estado de la cuestión caracterizado por diseños multimodales en los que variables tales como las calificaciones en las pruebas de ingreso de matemática, el género, el engagement con la carrera, o el lugar de procedencia, entre otras, son predictoras del rendimiento académico. En la tabla 1 se muestra un resumen de las principales variables que predicen, a partir de los estudios realizados, el rendimiento académico.

Tabla 1. Resumen de diversas variables que inciden en el rendimiento académico

  

Una vez realizado un recorrido por las principales investigaciones que centran su estudio en la predicción del rendimiento académico, los objetivos de esta investigación son:

Dentro de las asignaturas que se imparten en el primer año de la carrera Ingeniería en Ciencias Informáticas se encuentra la de Matemáticas Discretas, la cual desarrolla el pensamiento lógico y algoritmizador, elemento esencial de la especialidad de Ciencias Informáticas. La mayoría de los estudiantes tienen dificultades para aprender los contenidos de esta parte esencial de las matemáticas (Kularbphettonga, et al., 2015). De ahí el interés científico e institucional de conocer las variables que afectan al rendimiento de la misma.

 

METODOLOGÍA Y MÉTODOS

Población y muestra
La población está compuesta por 807 estudiantes matriculados en la asignatura Matemáticas Discretas de la carrera Ingeniería en Ciencias Informáticas de la República de Cuba, en el curso académico 2017-2018. De ellos 312 mujeres (38.66%) y 495 hombres (61.34%). Los datos fueron extraídos de la base de datos de la institución y de los resultados académicos oficiales del centro. 
Se realizó un muestreo aleatorio por conglomerados mediante el cual se seleccionaron 297 estudiantes, lo que representa el 36.80% de la población.
Variables
Variable dependiente: rendimiento académico en Matemáticas Discretas
Para ello se tuvo en cuenta la nota final de los estudiantes luego de su examen final y su examen extraordinario.
Variables independientes: sexo y provincia de procedencia
Ha sido una creencia generalizada durante varios cursos entre los profesores de la institución que los estudiantes de sexo masculino poseen mejor rendimiento académico que los de sexo femenino. De ahí lo interesante de validar o rechazar esta hipótesis. De igual forma resulta de interés conocer el impacto en el rendimiento dependiendo de la provincia de origen de los estudiantes.
Variables independientes: prueba de ingreso de matemática y opción en la que el estudiante solicitó la carrera
Debido a la importancia de la matemática en el desarrollo del pensamiento algorítmico, en la lógica y otros elementos necesarios para afrontar la Matemática Discreta, se considera conveniente aislar los efectos de este examen. Se tiene en cuenta además la opción en la que el estudiante solicita la carrera.
Variable independiente: materiales de estudio de la asignatura Matemática Discreta
Para ello se establecen, a partir del cuestionario aplicado, como subvariables de la variable materiales educativos las siguientes: capacidad de motivación, adecuación didáctica, relevancia del material y calidad tecnológica.
En la tabla 2 se observan las características de cada una de las variables independientes.
Tabla 2. Descripción de las variables independientes

Procedimiento
En la primera fase de la investigación se realizó un análisis descriptivo de cada una de las variables independientes de tipo intervalo incorporadas en el estudio. El objetivo es poder inferir características del conjunto de datos (población). Además, se realizó un análisis preliminar de la correlación existente entre las variables mediante un estudio correlacional de las mismas.
En segundo lugar, se utilizó un modelo de regresión lineal con datos de corte transversal, técnica estadística utilizada para explorar y cuantificar cómo influyen una o varias variables sobre otra, o incluso para predecir el valor de una variable basado en el conocimiento de otra u otras variables.
Mediante la regresión lineal múltiple por el método de mínimos cuadrados ordinarios se pretende crear un modelo matemático que permita pronosticar el bajo rendimiento académico en Matemática Discretas en la carrera Ingeniería en Ciencias Informáticas a partir de otras variables independientes (Chatterjee et al., 2015).
Finalmente, en la última parte del trabajo se determinó la dependencia de la probabilidad del estudiante de obtener un buen rendimiento académico en función de las variables independientes formuladas. Para ello se utilizó un modelo de regresión logística. Se debe convertir la variable dependiente a dicotómica, de tal forma que cuando la variable dependiente es 0 significa que el estudiante ha aprobado la asignatura (excelente, bien o regular). En caso contrario cuando el rendimiento académico es 1 significa que el estudiante posee un bajo rendimiento, es decir no ha aprobado la asignatura (mal).

RESULTADOS

En la tabla 3 se muestran los estadísticos descriptivos de las variables objetos de estudio con un tamaño muestral de N=297 estudiantes. En cuanto a la prueba de ingreso de matemática, el máximo es superior es 4, la media se sitúa en 2,81 puntos, existiendo una nota de corte de 1 para el acceso a los estudios universitarios, esto significa que todos obtuvieron al menos 60 puntos en el examen. Se destaca el valor de la opción en que solicitan la carrera Ingeniería en Ciencias Informáticas, con una media de 1,56 valor considerado positiva por los autores, puesto que refleja el interés mayoritario por la carrera. Por el contrario, los valores de las variables asociadas a materiales de estudio de la asignatura Matemáticas Discreta son a consideración de los autores, negativos. Obsérvese como la media ni siquiera llega a 3 (satisfecho).
Tabla 3. Estadísticos descriptivos de las variables de tipo intervalo

Nota: N número de participantes; DE: desviación estándar.
Coeficientes de correlación
Del estudio correlacional de las variables se extrae que las variables más correlacionadas con el rendimiento académico son: la prueba de ingreso de matemática y las asociadas a materiales de estudio, especialmente la capacidad de motivación, la adecuación didáctica y la calidad tecnológica de los materiales de estudio. Los otros pares de variables tienen unas correlaciones bajas y poco representativas (tabla 4). Ninguna de las correlaciones llega a valores superiores a 0,90, lo que indica que no existe multicolinealidad entre las variables.
Tabla 4. Coeficientes de correlación r de Pearson (N=297)

Nota: La correlación es significativa en el nivel ** menor o igual a 0,01(2 colas)

Modelo de regresión lineal múltiple
En este apartado de la investigación se realizó un análisis econométrico cuyo objetivo es detectar las variables predictoras del rendimiento académico. Se decidió desarrollar la regresión con todas las variables para identificar cómo se relacionan, además de comprobar la significación estadística de cada una de ellas.
Los estadísticos del modelo predictor muestran que cumple unos mínimos de robustez y significatividad en los parámetros estimados que lo hacen aceptable para realizar la predicción. El coeficiente de determinación R2 ajustado (0,63) indica una alta capacidad explicativa del modelo.
Los resultados detallados de la regresión para el modelo obtenido se exponen en la tabla 5. Del análisis de los coeficientes Beta estandarizados se podría afirmar que la variable más influyente en el rendimiento académico es la capacidad de motivación de los materiales de estudio (B=0,430). De similar relevancia resulta la variable resultados en la prueba de ingreso de matemática (B=0,319), lo que denota que estudiantes con mayores puntuaciones tienen mayores posibilidades de tener un buen rendimiento académico. Las demás variables, aunque en menor cuantía, poseen valor predictivo; excepto las variables, opción en que solicitaron la carrera y relevancia de los materiales de estudio que poseen un escaso valor predictivo.

Tabla 5. Resultado de la regresión en el modelo planteado

Variable dependiente: Rendimiento en Matemáticas Discretas.
Modelo de regresión logística
En la tabla 6 se puede observar que los indicadores generales del modelo determinaron que el conjunto de factores seleccionados contribuye significativamente a explicar la probabilidad de tener un bajo rendimiento académico, lo que se ve reflejado en el importante porcentaje de predicción correcto alcanzado (85.6%).
Tabla 6. Variable dependiente: rendimiento académico. Modelo de regresión logística

Predicción del modelo: 85,6%.
La variable que hace referencia a la provincia presenta un valor de odds-ratio (Exp(B)) muy próximo a la unidad (1,173), de manera que prácticamente no ejerce influencia en la probabilidad de conseguir (o no) un bajo rendimiento académico. Además de que su nivel de significación no cumple con los parámetros establecidos.
La variable que hace referencia al sexo posee un nivel de significación inferior a 0.05 (0,000) por lo que si influye en la variable dependiente. Su estimación de odds-ratio indica que los estudiantes varones tienen 2,091 menos posibilidades de suspender que las hembras, a igualdad en todas las demás condiciones.
La variable opción en que solicitó la carrera posee un nivel de significación superior a 0.05 por lo que se determina que no ejerce influencia significativa sobre el rendimiento académico. La variable que hace referencia a los resultados precedentes de la prueba de ingreso de matemática, nos está indicando que, en un estudiante con altas calificaciones de ingreso, se reduce la probabilidad de suspender Matemáticas Discretas en un 66%. 
Las variables asociadas a los materiales de estudio muestran variedad de resultados. Los estudiantes que perciben una alta capacidad de motivación con los materiales de estudio poseen cuatro veces más probabilidades de tener un buen rendimiento académico. Las variables asociadas a adecuación didáctica y calidad tecnológica de los materiales indican que aquellos estudiantes que las valoran con mayor nivel, poseen aproximadamente 20% menos de probabilidad de alcanzar un bajo rendimiento académico, con respecto al resto de sus compañeros. En cuanto a la relevancia de los materiales de estudio, esta variableposee un nivel de significación superior a 0,05; por lo que no ejerce influencia significativa sobre el rendimiento académico.

Figura 1.Potencial predictivo de las variables del modelo

 

 

 

 

 

 

 

 

 

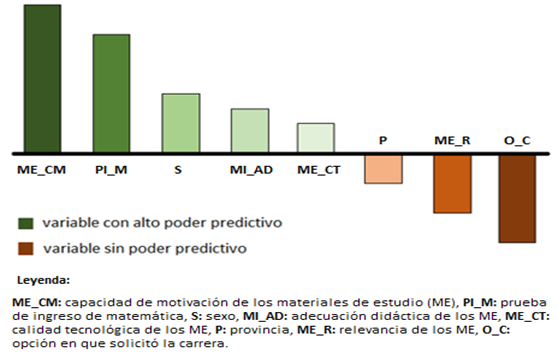
DISCUSIÓN

Los resultados obtenidos en esta investigación aportan una visión de los factores que tienen un valor predictivo en el rendimiento académico en Matemáticas Discretas en los estudiantes de Ciencias Informáticas. De todas las variables independientes que se valoraron, las que demostraron poseer una relación más fuerte en la predicción del rendimiento académico, fueron la calificación obtenida en la prueba de ingreso de matemática y la capacidad de motivación de los materiales de estudio.
Al igual que otras investigaciones el presente trabajo ha puesto de manifiesto, que la variable sexo es estadísticamente significativa a la hora de predecir el rendimiento académico en Matemáticas Discretas para la carrera Ingeniería en Ciencias Informáticas (Treviño et al., 2017). No sucede así con la variable opción en la que el estudiante solicita la carrera. Aunque en principio podría parecer inconsistente desde el punto de vista motivacional, todo parece indicar que los estudiantes solicitan la carrera sin conocer a ciencia cierta las interioridades de la misma.
Si bien quedó demostrado que el rendimiento académico va asociado a un buen dominio en el área de la matemática y a los materiales de estudio, existen también otros factores, no tratados en este trabajo, tales como los hábitos de estudios, la asistencia regular a clases, el trabajo independiente y no menos significativa las ganas de aprender, que pudieran tener un rol importante a la hora de analizar los factores asociados al rendimiento académico (Garbanzo, 2014; Castellanos et al., 2017).

 

CONCLUSIONES

Se puede concluir que la calidad del modelo predictivo presentado es adecuada, por lo que permite informar positivamente a los profesores y directivos docentes sobre el rendimiento académico que se espera de sus estudiantes. Estos resultados contribuyen al desarrollo de acciones diferenciadas con los estudiantes; tales como: a) proponer materiales de estudio con alta capacidad de motivación y diversificar su uso según las necesidades de los estudiantes, b) equilibrar los grupos de estudiantes en función del rendimiento y diseñar acciones diferenciadas para aquellas que tienen más probabilidades de no superar la asignatura objeto de estudio.

 

REFERENCIAS BIBLIOGRÁFICAS

Barker, N. (2014). Students who are deaf and hard of hearing in California:  A cross-sectional analysis. ProQuest Dissertations and Theses Global: Social Sciences. Disponible en: http://search.proquest.com/docview/1554346198?accountid=14542 

Broc, M.A. (2016). La predicción del rendimiento académico en alumnos de bachillerato. Estudio de un caso (centro) en España. European Journal of Scientific Research. 12 (25), 111-130.

Castellanos, V., Latorre, D., Mateus, S., & Navarro, C. (2017). Modelo explicativo del desempeño académico desde la autoeficacia y los problemas de conducta. Revista Colombiana de Psicología, 26(1), 149-161.

Chaparro, A., González, C. y Caso, J. (2015). Familia y rendimiento académico: configuración de perfiles estudiantiles en secundaria. Revista Electrónica de Investigación Educativa. 18(1), 1-17.

Chatterjee, S., Guntuboyina, A., y Sen, B. (2015). On risk bounds in isotonic and other shape restricted regression problems. The Annals of Statistics, 43 (2015), no. 4, 1774--1800.

Choi, J. & Hwang, J. (2017). The effect of school choice on student´s academic performance. Hitotsubashi Journal of Economics, 58 (1), 1-19.

Flores-Hernández, F., Sánchez-Mendiola, M., & Martínez-González, A. (2016). Modelo de predicción del rendimiento académico de los estudiantes del ciclo básico de la carrera de medicina a partir de la evaluación del desempeño docente. Revista Mexicana de Investigación Educativa, 21 (70), 975-991.

Garbanzo, G. (2014, enero-abril).  Factores asociados al rendimiento académico tomando en cuenta el nivel socioeconómico: Estudio de regresión múltiple en estudiantes universitarios. Revista Electrónica Educare, 18 (1), 119-154.

Gil, María del C., García, Cristina M., y Manrique, Miguel A. (2017). El poder de las expectativas del docente en el logro académico de los escolares inmigrantes. Revista de Pedagogía, 38 (102), 1-25.

González, A., y Valenzuela, J. (2016). Factores motivacionales y construcción de aspiraciones de estudios universitarios: evidencia de un contexto regional chileno. Revista de Pedagogía, 37 (100). 111-134.

Gotzens, C., Cladellas, R., Clariana, M., y Badia, M. (2015). Indisciplina instruccional y convencional: su predicción en el rendimiento académico. Revista Colombiana de Psicología, 24 (2), 317-330.

Hamsa, H., Indiradevi, S., & Kizhakkethottam, J. (2016). Student academic performance prediction model using decisión tree and fuzzy genetic algorithm. En Global Colloquium in Recent Advacement Effectual Researchers in Engineering, Science and Technology (RAEREST 2016), 326-332

Jamba-Joyner, J., y Klostermeyer, W. (2003). Predictors for success in a discrete math course. ACM SIGCSE Bulletin, 35 (2), 66-69.

Katsikas, E., y Panagiotidis, T. (2010).  Student status and academic performance: an approach of the quality determinants of university studies in Greece. The European Institute, GreeSE Paper, 40, 1-45.

Kularbphettonga, K., Putglana, R., Tachpetpaiboona, N., Tongsirib, C., y Roonrakwitb, P. (2015). Developing of mLearning for Discrete Mathematics based on Android Platform.  Procedia - Social and Behavioral Sciences (197), 793-796.

Marschark, M. (2015). Predicting the academic achievement of deaf and har-of-hearing students from individual, household, communication and educational factors. Exceptional Children, 81 (3), 350-369.

Mediavilla, M., y Gallego, L. (2016). Condicionantes del rendimiento académico en la escolaridad primaria en Brasil: un análisis multifactorial. Educ. Soc., Campinas, 37 (134), 195-216.

Mora, R. (2015). Factores que intervienen en el rendimiento académico universitario: Un estudio de caso. Opción (6), 1041 - 1063.

Palomar, J., & Estrada, A. V. (2016). Factores explicativos del rendimiento académico en hijos de inmigrantes mexicanos en Nueva York. Psicología Educativa, (22), 125-133.

Pinxten, M., Marsh, H., De Fraine, B., Van Den Noortgate, W., y Van Damme, J. (2014). Enjoying mathematics or feeling competent in mathematics? Reciprocal effects on mathematics achievement and perceived math effort expenditure. British Journal of Educational Psychology, 84 (1), 152-174.

Pokropek, A,. Borgonovi, F,. y McCormick, C. (2017). On the Cross-Country Comparability of Indicators of Socioeconomic Resources in PISA. Applied Measurement in Education, 30 (4), 243-258.

Presentacion, M., Siegenthaler, R., Pinto, V., Mercader, J., y Miranda, A. (2015). Math kills and executive functioning in preschool: Clinical and ecological evaluation. Revista de Psicodidáctica, 20 (1), 65-85.

Reimann, G., Stoecklin, M., Lavallee, K., Gut, J., Frischknecht, M., y Grob, A. (2013). Cognitive and motivational profile shape predicts mathematical skills over and above profile level. Psychology in the Schools, 50 (1), 37-56.

Saw, G., Schneider., Frank, K., Chen, I., Keesler, V., y Martineau, J. (2017). The Impact of Being Labeled as a Persistently Lowest Achieving School: Regression Discontinuity Evidence on Consequential School Labeling. American Journal of Education, 123 (4), 585-613.

Soria-Barreto, K., y Zúñiga-Jara, S. (2014). Aspectos determinantes del Éxito académico de estudiantes universitarios.  Formación Universitaria, 7 (5), 41-50.

Stinebrickner, T., y Stinebrickner, R. (2003). Working during school and academic performance. Journal of Labor economics, 21 (2), 473-491.

Treviño, Len J., Balkin, David B., y Gomez-Mejia, Luis R. (2017) How “Doing Gender” Leads to Gender Imbalances in the Higher Ranks in Colleges of Business [And How To “Undo Gender”]. Academy of Management Learning and Education,16 (3), 439-453.

Vargas, M., y Montero, E. (2016). Factores que determinan el rendimiento académico en matemáticas en el contexto de una universidad tecnológica: aplicación de un modelo de ecuaciones estructurales. Universitas Psychologica, 15 (2).

Vergel-Ortega, M., Martínez-Lozano, J., y Zafra-Tristancho, S. (2016). Factores asociados al rendimiento académico en adultos. Revista Científica, 25, 206-2015.

Yarnel, M., y Bohrnstedt G. (2017). Student-Teacher Racial Match and Its Association With Black Student Achievement: An Exploration Using Multilevel Structural Equation Modeling. American Educational Research Journal, doi: 10.3102/0002831217734804

 

Datos del (los) autor (es)

¹Ingeniero en Ciencias Informáticas. Máster en Ciencias Matemáticas. Estudiante del Doctorado en Ciencias de la Educación de la Universidad de Sevilla (España). Profesor Auxiliar. Jefe del Departamento de Inteligencia Computacional de la Universidad de las Ciencias Informáticas (Cuba). Miembro de la Sociedad Cubana de Matemática y Computación y de la Asociación Nacional de Pedagogos de Cuba. ORCID-ID 0000-0002-9701-9351.

²Doctora en Ciencias de la Educación. Profesora Titular del Departamento de Métodos de Investigación y Diagnóstico en Educación de la Universidad de Sevilla (España). Investigadora del Grupo de Investigación "Investigación, Evaluación y Tecnología Educativa" (http://giete.us.es). Miembro de la Red Universitaria de Investigación e Innovación Educativa REUNID+D (http://reunid.eu). Editora-Jefe de la Revista Fuentes https://revistascientificas.us.es/index.php/fuentes/index . ORCID-ID 0000-0001-8738-565X.

 

Recibido: 15 de mayo de 2019
Evaluado: 26 de octubre de 2019
Aceptado para su publicación: 14 de noviembre de 2019