INTRODUCCIÓN

Los resultados del examen de ingreso del Centro Nacional de Evaluación para la Educación Superior (CENEVAL) hacen patente que muchos estudiantes de la Universidad Veracruzana (UV), México, no poseen (CENEVAL, 2017) un nivel adecuado de conocimientos en las siguientes áreas: (i) habilidad verbal, (ii) habilidad matemática y (iii) el área de matemáticas que evalúa el conocimiento matemático propiamente dicho.
Esta exploración, de carácter cuantitativo, no explica las causas de la falta de competencias del estudiante que ingresa a los estudios universitarios. Sin embargo, investigaciones recientes en la UV ponen de manifiesto dificultades en comprensión del concepto de variable (Herrera, Cuesta & Escalante, 2016), así como la ausencia de significados en los estudiantes sobre los conceptos de velocidad, distancia recorrida y pendiente de recta, cuando se enfrentan a tareas sobre situaciones contextualizadas de manera verbal y/o gráfica (Cuesta, Escalante & Ruíz, 2016).
De este modo, y con el objeto de obtener información cualitativa para el diseño de unidades didácticas que coadyuven al proceso de aprendizaje, el equipo docente propuso realizar una investigación para constatar la problemática relativa al nivel de comprensión del estudiante sobre situaciones escolares, así como conocer sus habilidades elementales de cálculo numérico–algebraico y sus destrezas y aptitudes para la representación de relaciones cuantitativas.
Se propone diseñar y aplicar una prueba escrita (evaluación de tipo diagnóstico), compuesta por problemas sobre situaciones contextualizadas; el objetivo es conocer, tanto el nivel de conocimientos sobre los conceptos como la forma en que el estudiante aborda la solución de las situaciones planteadas.
La prueba, compuesta por 14 problemas típicos de contexto escolar, debe dar respuesta a dos interrogantes: (i) ¿qué dificultades muestran los estudiantes universitarios cuando se enfrentan a tareas escolares? y (ii) ¿influye el nivel de avance curricular, el contexto de las situaciones y su grado de dificultad en el nivel de respuesta del estudiante?
La investigación en educación matemática, que abordan el estudio de los problemas en el proceso de transición de la aritmética al álgebra, ha legado enseñanzas y experiencias invaluables (Arcavi, 2013), situando al lenguaje algebraico como una herramienta para expresar relaciones y derivar conclusiones en el tránsito entre la manipulación simbólica y sus significados. Pero también pone de manifiesto que se recurre al uso de procedimientos aritméticos en lugar del método algebraico; situación que, al manifestarse en todos los aspectos que caracterizan el campo conceptual del álgebra (Socas, Palarea & Hernández, 2013), induce al estudiante a trasladar sus dificultades desde un nivel educativo a otro. No se tiene un conocimiento estructural del Álgebra, en tanto que se aborda, casi siempre, desde un conocimiento de tipo procedimental.
Otra investigación (Escalante & Cuesta, 2013) analiza la comprensión asociada al proceso de traducción de los lenguajes natural, aritmético y geométrico al lenguaje algebraico. Estudio que exhibe la existencia de errores y dificultades asociadas al desarrollo cognitivo del estudiante, quien no ha desarrollado la capacidad de utilizar el concepto matemático en situaciones contextualizadas, aun cuando éstas formen parte de sus experiencias personales y conocimientos anteriores.
Es preciso destacar que, las dificultades en el aprendizaje de la matemática tienen naturaleza distinta; una de ellas se halla en la complejidad de los objetos matemáticos y se relaciona, tanto con las formas de representar dichos conceptos como con las relaciones que se establecen entre esas representaciones (Lupiañez, 2013).
El término representación es complejo, en tanto que enclaustra diversos significados y puede ser utilizado en una gran variedad de ámbitos; sin embargo, su exhaustiva clarificación (Rico, 2009), en educación matemática, permite concebirlo como parte esencial del aparato conceptual necesario para analizar los procesos de aprendizaje y comprensión de las matemáticas.
Las representaciones constituyen el conjunto de “notaciones simbólicas o gráficas, mediante las que se expresan conceptos y procedimientos matemáticos, así como sus características y propiedades más relevantes” (Castro & Castro, 2000, p. 96) que se clasifican en registros de representación (Duval, 1999) y de cuya comprensión depende de si la representación mental es parte de una red de representaciones (Martí & Pozo, 2000; Hitt, 2001; Rico, 2009). Es importante destacar el término comprensión:
“Comprender significa percibir mentalmente algo, captar el significado de algo, entender con claridad lo que quiere decir alguien, conocer en un objeto todo lo que de él es concebible, llegar a conocer la naturaleza o modo de ser de una cosa” (Rico, 2009, p. 2).
Además de la representación y de los errores que se cometen con las mismas, entendemos que el significado de un concepto incluye una perspectiva semántica, que se compone por el signo con el que se expresa el concepto, su referencia y el sentido que se le atribuye cuando se usa. En matemática escolar, (Rico, 2012) identifica estas tres componentes:

• Signo con sistemas de representación, o conjunto de símbolos y reglas con las que se representa el concepto.
• Referencia con estructura conceptual, la cual engloba las propiedades del concepto, los argumentos y proposiciones derivadas y los criterios de veracidad.
• Sentido con fenomenología, contextos, situaciones o problemas que dan sentido al concepto.

De acuerdo con lo anterior, el sentido de un contenido (Flores, Moreno & Del Río, 2016) lo marcan los términos que se emplean para referirse al contenido, las situaciones que se poden en marcha, los usos que se le dan en estas situaciones y los fenómenos que históricamente se han organizado a través de dicho contenido. Por ello, su análisis (Flores, et al, 2016) abarca el estudio de las estructuras conceptuales, evolución histórica, sistemas de representación y modelos, y análisis fenomenológico.
En este sentido (Duval, 1999) existe una actividad que se vincula a la producción de representaciones (semiosis) y otra ligada a la aprehensión conceptual de un objeto (noesis). La teoría del Profesor Raymond Duval establece que un sistema semiótico es un sistema de representación si permite la realización de tres actividades: (i) la identificación de la presencia de una representación, que implica la selección del rasgo del contenido a representar, (ii) el tratamiento de una representación o transformación interna dentro de un mismo sistema y (iii) la conversión o transformación de una representación en otra de otro sistema, conservando una parte o la totalidad del contenido de la primera.
De este modo, la actividad cognitiva en matemática (Duval, 1999) recurre a varios registros de representación semiótica, sea ésta una producción discursiva (lenguaje natural o formal) o no discursiva (figura, gráfico o esquema). Traslado que puede dar lugar a fenómenos de congruencia y no congruencia semántica; cuando no hay congruencia la tarea puede ser muy difícil y no accesible para muchos estudiantes.

Metodología y métodos

La investigación es de corte cualitativo, con el objeto de conocer y analizar los modos de resolución y dificultades de los estudiantes universitarios, cuando responden a problemas donde se manifiestan procesos de generalización y de modelación a través de la relación del lenguaje algebraico con los lenguajes figural, natural y aritmético. El análisis está orientado a tareas que estaban directamente relacionadas con el proceso de transformación y/o conversión entre representaciones en diferentes lenguajes: natural, aritmético, figural y algebraico.
Sujetos de la experiencia:
Con la finalidad de realizar una comparación entre dos grupos, con diferentes niveles de avance dentro de la universidad, se realizó la toma de dos muestras de estudiantes mediante un muestreo no probabilístico (por conveniencia). Las muestras (Ver Tabla 1) se diferencian por el nivel de avance curricular, es decir, diferencias significativas en cuanto a los conocimientos adquiridos de matemática en la universidad.
La primera (en lo sucesivo Grupo 1): La población está compuesta por 96 estudiantes de la Licenciatura en Tecnologías Computacionales (TC), que se caracteriza por haber cursado, y aprobado, solamente dos experiencias educativas (asignaturas): Fundamentos de Matemática y Álgebra Lineal. De ella se seleccionan 29 estudiantes (30%).
La segunda (en lo sucesivo Grupo 2): La población está compuesta por 60 estudiantes de la Licenciatura en Economía, que se caracterizada por haber cursado ocho experiencias (asignaturas) de matemática en la universidad. De ella se seleccionan 21 estudiantes (35%).
Debido a la evidente necesidad de mantener la confidencialidad, a los estudiantes se les asigna un código de referencia (Ver Tabla 1).

Tabla 1: Composición de la muestra.

Grupo	Cursos Aprobados	Temáticas recibidas	Número de Estudiantes	Cód.
1	Fundamentos de Matemática y Álgebra Lineal	Aritmética y álgebra, Lógica y teoría de conjuntos, Algebra matricial y vectorial	29	T1 - T29
2	Fundamentos de Matemática, Álgebra Lineal Cálculo I Cálculo II Estadística, Probabilidad. Econometría I Econometría II	Aritmética y álgebra, Lógica y teoría de conjuntos, Algebra matricial y vectorial, Optimización en una y varias variables, Optimización con restricciones, Probabilidad, Estadística, Análisis de regresión y correlación, Series de Tiempo, Series estacionarias y no estacionarias	21	E1.- E21

Fuente: Elaboración propia

El instrumento de evaluación:
Se diseñó una prueba escrita compuesta por 14 tareas escolares, en las que se requiere ejecutar el tratamiento (transformación interna) y/o la conversión (transformación de una representación en otra de otro sistema). Se parte de la competencia en el proceso del paso de un texto escrito (lenguaje natural) a un texto escrito en el lenguaje aritmético o algebraico.
Categorías de análisis
Se clasifican las actuaciones correctas y erróneas, categorizadas por la manifestación de alguna de las siguientes categorías:
Por el nivel de comprensión:
Incomprensión: concentra las actuaciones, donde se observa que no se comprende el enunciado y/o la tarea a realizar y/o los conceptos involucrados en la situación.
Interpretación inadecuada: resume aquellas, donde existe comprensión pero con una interpretación errada de las condiciones del problema.
Por la conversión de un sistema de representación a otro:
Representa en lenguaje aritmético: se traduce al lenguaje aritmético (registro en lenguaje aritmético), seguido de transformaciones internas (operaciones elementales) para llegar a la solución de la tarea.
Representa en lenguaje algebraico: a partir del registro en lenguaje natural, o del registro en lenguaje aritmético, se expresan relaciones algebraicas entre las cantidades desconocidas (registro en lenguaje algebraico), seguido de un tratamiento interno para llegar a la solución.

RESULTADOS

Para analizar las actuaciones de los estudiantes (modos de hacer y conducirse) (Rico & Lupiáñez, 2010) se propone la prueba, compuesta por 14 situaciones típicas de contexto escolar, cuyos contendidos fueron estudiados en niveles anteriores a la universidad. A afectos de este trabajo trataremos algunas de ellas, específicamente las situaciones: 5, 6 y 12 de la prueba.
El análisis de las respuestas se realizó utilizando el método de análisis de contenido, entendido como el análisis riguroso, el examen y verificación de los contenidos en datos escritos, y cuya finalidad es descubrir la estructura interna de la comunicación, estudiando para ello su contenido semántico (Cohen, Manion & Morrison, 2011); (Rico y Fernández-Cano, 2013).
Situación 5: En un teatro las entradas para adultos costaban $5 y para niños $2. Concurrieron 326 espectadores y se recaudaron $1090. ¿Cuántos espectadores eran adultos? ¿Cuántos eran niños?
La primera dificultad se manifiesta en el intento por realizar una conversión al lenguaje aritmético, seguido de operaciones con base al procedimiento de prueba y error (Ver Figura 1) que no les permite llegar a la solución algebraica del problema.

Figura 1

Fuente: Anotaciones del estudiante E19 a situación 5

Cabe destacar que, la mayoría de los estudiantes logra reconocer e identificar la presencia de valores desconocidos, pero una proporción significativa de los estudiantes (30% del Grupo 1 y 25% del Grupo 2) se halla ante el obstáculo asociado al proceso de conversión del problema (representado en lenguaje natural) a un registro en otro sistema semiótico (lenguaje aritmético o algebraico).
Otros estudiantes se hallan ante la dificultad para comprender las condiciones del problema, por el hecho de que no se logra identificar la presencia de una representación en lenguaje natural. Obsérvese que el estudiante (Ver Figura 2) no es capaz, incluso, de estructurar una idea sobre lo que se solicita como tarea.

Figura 2

 

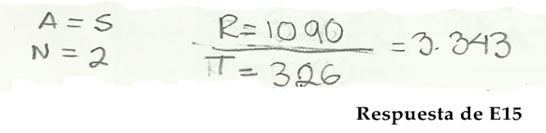
Fuente: Anotaciones del estudiante E15 a situación 5

Situación 6: A un aficionado a los rompecabezas le preguntaron cuántos años tenía. La contestación fue: “Toma tres veces los años que tendré dentro de tres años, réstale tres veces los años que tenía hace tres años y resultará exactamente los años que tengo ahora”. ¿Cuántos años tiene ahora?
En algunas actuaciones (15% del Grupo 1 y 10% del Grupo 2) se pone de manifiesto la incomprensión del enunciado y/o de la tarea a realizar, provocado por una combinación de los diferentes sentidos que el estudiante atribuye a partir de su lectura personal. En primer lugar, destaca la dificultad para expresar las condiciones del problema en lenguaje aritmético y/o algebraico (Ver Figura 3).

Figura 3

Fuente: Anotaciones del estudiante E16 a situación 6

Obsérvese que, el estudiante E16 afirma no poder responder a la pregunta porque no tiene lo que él denomina “datos”. La lectura personal, que realiza, no le permite identificar la relación entre las cantidades (desconocidas y conocidas), a causa de la falta de asociaciones entre las representaciones semióticas expresadas en registro verbal.

Desde las actuaciones de otros estudiantes se observa la interpretación de las condiciones del problema, tal como muestra la respuesta T23 (Ver Figura 4).

Figura 4

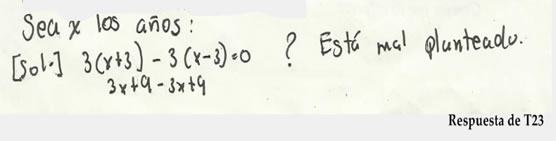
Fuente: Anotaciones del estudiante E16 a situación 6

Obsérvese que logra representar parte del enunciado en lenguaje algebraico para luego reconocer que está “mal planteado”, debido a la necesidad de igualar a cero. Un hábito que proviene de sus experiencias personales, relacionadas con la solución de ejercicios rutinarios, en los que se tiene que igualar a cero para llegar a la respuesta: un problema típico de las clases de matemática.
Situación 12: De una torta Juan se comió la mitad, Luisa la tercera parte, y Pedro la cuarta parte. ¿Es esto posible? Justifica tu respuesta.
Esta tarea de reparto (Real, Gómez, & Figueras, 2014) exige que el estudiante establezca tres fracciones parte todo y determine, mediante operación aritmética, si es posible el reparto por comparación de la suma de partes con el todo (la unidad). Para algunos estudiantes (35% del Grupo 1 y 28% del Grupo 2) resultó un obstáculo transformar (Ver Figura 5) las condiciones del problema (registro en lenguaje natural) a otra representación en lenguaje aritmético.
Como no se tiene el sentido y significado de la noción de “fracción”, en una tarea de reparto, el estudiante realiza una lectura literal que conduce a un dibujo (lenguaje figural) de la torta.

Figura 5

Fuente: Anotaciones del estudiante T22 a situación 6

Discusión

Aun cuando analizar las dificultades de comprensión lectora no fue uno de los propósitos de investigación, se constató que la primera y principal dificultad emerge de la incomprensión del enunciado y/o del contexto del problema. Situación que varía dependiendo del nivel de complejidad de los problemas y del instrumental matemático que el estudiante considera disponible y pertinente.
La segunda dificultad es causada por el sentido personal del estudiante sobre los conceptos que fueron objeto de estudio con anterioridad. Muchas respuestas se asocian a imágenes visuales (prototipos) que se han utilizado en el proceso de enseñanza, como ejemplos “clarificadores” para exponer un modelo sobre dichos conceptos.
En tercer lugar, destaca el uso generalizado de procedimientos aritméticos de naturaleza instrumental y memorística, sin la competencia para transferir dicho conocimiento (sobre el contexto y su solución aritmética) a una expresión algebraica.
Otro aspecto significativo es que, sin importar el nivel de avance se recurre por igual al uso de estos procedimientos con una fuente de significado muy limitada que no resulta suficiente para aplicar procedimientos de generalización algebraica. Resultados que muestran la existencia de errores (Ortega y Pecharromán, 2014) en la medida que los alumnos van adquiriendo los conceptos en diferentes estadios de aprendizaje (semiótico, estructural y autónomo).
Los estudiantes más avanzados (de la licenciatura en economía) no poseen mayor nivel de comprensión de los problemas propuestos. Por el contrario, para un alto porcentaje de estudiantes de 8vo semestre existe el obstáculo asociado al proceso de conversión del problema (representado en lenguaje natural) a un registro en otro sistema semiótico (lenguaje aritmético o algebraico).
Queda demostrado que el estudiante de economía no comprende mejor los problemas, únicamente se vale de más recursos de carácter procedimental, por el hecho de haber cursado más estudios de matemática dentro de la universidad. Debido, y en primer lugar, a la carencia de conocimientos y/o a la falta de habilidad para estructurar la información en lenguaje natural; en otras palabras, el estudiante no logra captar el sentido del planteamiento y/o de la relación entre variables.

CONCLUSIONES

En este estudio, de corte cualitativo se propusieron dos preguntas de investigación, a saber: ¿qué dificultades muestran los estudiantes universitarios cuando se enfrentan a tareas escolares? e ¿influyen el nivel de avance curricular, el contexto de las situaciones y su grado de dificultad en el nivel de respuesta del estudiante? Se hallaron relevantes indicios sobre la existencia de dificultades comunes en ambos grupos de estudiantes. Los hechos observados son:

• El estudiante no posee competencia para comprender textos aritmético-algebraicos de enunciado verbal; es decir, no existe una lectura analítica del enunciado del problema que lo reduzca a una lista de cantidades y de relaciones entre cantidades.

• El nivel de conocimiento sobre el concepto es tan elemental, que no se asocia éste a situaciones o problemas que le den sentido.

• No se muestra la competencia para realizar el tratamiento de una misma representación (transformación interna), como tampoco para realizar la conversión necesaria de una representación en otra de otro sistema.

• Existe la tendencia a utilizar formalismos de tipo algebraico, descontextualizados y no comprendidos, que no son útiles al estudiante en la solución de los problemas.

Los estudiantes de economía presentan los mismos problemas de comprensión lectora que los estudiantes de Tecnologías Computacionales. Los resultados comparativos dejan de manifiesto un hecho: el nivel académico formal no ha implicado un aprendizaje significativo, que coadyuve a la comprensión del contenido de los problemas. Persisten las dificultades en la transición de la aritmética al álgebra y en la traducción del lenguaje natural al algebraico, que no permite los procesos de generalización. Los estudiantes universitarios presentan una seria dificultad para comprender la estructura general del problema, a partir de las cantidades (conocidas y desconocidas) y se pone de manifiesto que el nivel de avance curricular no mejora el proceso de transferencia de ideas expresadas en los lenguajes natural y aritmético al lenguaje algebraico. De este modo, y más allá de las carencias relativas a las técnicas, se constata que conceptos fundamentales no han sido construidos de manera satisfactoria, lo cual constituye un obstáculo para abordar analíticamente el estudio de la matemática universitaria. En este estudio se hallaron relevantes indicios sobre la existencia de dificultades en el tránsito, desde la educación básica y media superior a la educación superior; hallazgos que sugieren la necesidad de continuar con otros estudios que incursionar en la comprensión asociada al proceso de traducción de los lenguajes natural, aritmético y geométrico al lenguaje algebraico.

REFERENCIAS BIBLIOGRÁFICAS

 Arcavi, A. (2013). Reflexiones sobre el álgebra escolar y su enseñanza. En L. Rico, M.C. Cañadas, J. Gutierrez, M. Molina & I. Segovia. (Editores). Investigation en Educación Matemática. Homenaje a Encarnación Castro (Pp. 13 - 22) Granada, España: Editorial Comares. 
Castro, E. & Castro, E. (2000). Representaciones y modelización. En L. Rico (Ed.), La educación matemática en la enseñanza secundaria 2da Edición (pp. 95-124). Barcelona, España: Horsori.
CENEVAL. (2017). Examen Nacional de Ingreso a la Educación Superior. EXANI-II. UV. Recuperado de: https://www.uv.mx/blogs/sea/category/convocatoria-para-examen-de-nuevo-ingreso/
Cohen, L., Manion, L., & Morrison, K. (2011). Research methods in education. Londres, Reino Unido: Routledge.
Cuesta, A. Escalante, E. & Ruiz, J. F. (2016). Velocidad. Significados manifestados por estudiantes universitarios a partir de representaciones gráficas. AIEM - Avances de Investigación en Educación Matemática (Nro. 9), pp. 105 – 125. Recuperado de http://www.aiem.es/index.php/aiem
Duval, R. (1999). Semiosis y pensamiento humano. Registros semióticos de aprendizajes intelectuales. Cali, Colombia: Edit. Universidad del Valle.
Escalante, J. & Cuesta, A. (2013). Dificultades para comprender el concepto de variable: un estudio con estudiantes universitarios. Educación Matemática. (Nro. 24-1), pp.5– 30. Recuperado de http://www.revista-educacion-matematica.org.mx/revista/
Flores, P. Moreno A. & Del Río A. (2016). Análisis didáctico en formación inicial de profesores. En E. Castro, E. Castro, J. L. Lupiáñez, J.F. Ruiz & Torralbo, M. (Editores). Investigación en Educación Matemática. Homenaje al profesor Luis Rico (Pp. 141-151)
Gómez, B., & García, A. (2014). Competencias de los estudiantes en razón y proporción: El caso de las tareas de relativizar. En J. L. González, J. A. Fernández-Plaza, E. Castro-Rodríguez, M. T. Sánchez-Compaña, C. Fernández, J.L. Lupiáñez y L. Puig (Editores.), Investigaciones en Pensamiento Numérico y Algebraico e Historia de las Matemáticas y Educación Matemática (Pp. 83-91). Málaga, España: Departamento de Didáctica de las Matemáticas, de las Ciencias Sociales y de las Ciencias Experimentales y SEIEM.
Herrera, H. Cuesta, A. & Escalante, J.E. (2016). El concepto de variable: un análisis con estudiantes de bachillerato. Educación Matemática, (Nro. 28-3),pp. 217- 240. Recuperado de http://www.revista-educacion-matematica.org.mx/revista/
Hitt, F. (2001). El papel de los esquemas, las conexiones y las representaciones internas y externas dentro de un Proyecto de Investigación en Educación Matemática. En P. Gómez y L. Rico (Editores.), Iniciación a la investigación en didáctica de la matemática. Homenaje al profesor Mauricio Castro (Pp. 165-177). Granada, España: Universidad de Granada.
Lupiañez, J. L. (2013). Análisis didáctico: La planificación del aprendizaje desde una perspectiva curricular. En L. Rico, J. L. Lupiañez & M. Molina (Editores.). Análisis Didáctico en Educación Matemática (pp. 81 - 101). Granada, España: Comares.
Martí, E., & Pozo, J. I. (2000). Más allá de las representaciones mentales: la adquisición de los sistemas externos de representación. Infancia y aprendizaje: Journal for Study of Education and Development (Nro. 23-90), pp. 11-30.
Ortega, T. y Pecharromán, C. (2014). Errores en el aprendizaje de las propiedades globales de las funciones. Revista de investigación en educación (Nro. 12-2) pp. 209-221.
Real, R., Gómez, B. & Figueras, O. (2014). Aspectos de la fracción en los modelos de enseñanza: El caso de un libro de texto.  Épsilon - Revista de Educación Matemática (Nro. 85), pp. 21-36. Recuperado de http://thales.cica.es/epsilon/sites/thales
Rico, L. (2009). Sobre las nociones de representación y comprensión en la investigación en educación matemática. PNA (Nro. 4-1),pp. 1- 4
Rico, L. (2012). Aproximación a la investigación en Didáctica de la Matemática. Avances en Investigación en Educación Matemática. (Nro. 1),pp.39-63. Recuperado de http://www.aiem.es/index.php/aiem
Rico, L. & Lupiáñez, J. L. (2010). Objetivos y competencias en el aprendizaje de los números naturales. UNO: Revista de Didáctica de la Matemática, (Nro. 54), pp. 14-30. Recuperado de http://funes.uniandes.edu.co/1755/
Rico, L. y Fernández-Cano, A. (2013). Análisis didáctico y metodología de investigación. En L. Rico, J.L. Lupiáñez y M. Molina (Editores.), Análisis Didáctico en Educación Matemática (pp. 1-22). Granada, España: Comares.

Socas, M. M., Palarea, M. M. & Hernández, J. (2013). Dificultades y uso de los recursos algebraicos de estudiantes para maestros de educación primaria. En L. Rico, M. C. Cañadas, J. Gutiérrez, M. Molina & I. Segovia (Editores.). Investigación en Didáctica de la Matemática. Homenaje a Encarnación Castro (Pp. 95 - 102). Granada, España:

Datos del (los) autor (es)

¹Doctor en Didáctica de la Matemática. Universidad Autónoma de Barcelona, España, Docente de Tiempo Completo de la Facultad de Economía de la Universidad Veracruzana, México.