Revista Atenas. ISSN: 1682-2749. Nro. 62 (2024) enero-diciembre págs.[1 - 15] https://atenas.umcc.cu
El núcleo básico del pensar como proceso y su lugar en la resolución de problema
The core of thinking as a process and its place in problem solving
O núcleo básico do pensar como processo e seu lugar na resolução de problemas
Artículo de investigación
Recibido: 19/07/2024 Evaluado: 22/08/2024 Aceptado: 06/09/2024
Maritza Petersson Roldán
Universidad de Ciencias Médicas. Matanzas, Cuba.
https://orcid.org/0000-0002-0453-3571
petersson.roldan@gmail.com
Arnaldo Vicente Morey Ramos
Universidad de Matanzas, Cuba.
https://orcid.org/0000-0003-4589-4856
arnaldo.morey@umcc.cu
¿Cómo citar el artículo?
Petersson-Roldán, M. & Morey-Ramos, A. V. (2024). El núcleo básico del pensar como proceso y su lugar en la resolución de problemas. Atenas, nro. 62, e10423, 1-15.
Resumen
En la enseñanza de la Física la resolución de problemas se constituye en un objeto esencial de aprendizaje. La presente investigación tuvo como objetivo proponer un sistema de actividades en el curso de Física para la Carrera de Ingeniería Química que contribuya al desempeño de los estudiantes en la resolución de problemas a partir de potenciar el desarrollo del análisis a través de la síntesis. La investigación asumió el paradigma de investigación cualitativo, mediante un método de investigación acción pedagógica y una intervención didáctica a través de un sistema de actividades. La sistematización de diferentes enfoques en el tratamiento del tema y la valoración del papel del análisis a través de la síntesis como núcleo básico del pensar sirvieron de fundamento para el diseño de la propuesta, que fue validada después de su implementación a través de una estrategia pretest-postest. Se concluye que el nivel del análisis a través de la síntesis en los estudiantes puede ser mejorado con intervenciones intencionadas a tales propósitos.
Palabras clave: Resolución de problemas; análisis a través de la síntesis; enseñanza de la Física; Indicadores de desarrollo del análisis a través de la síntesis.
Abstract
In the teaching of Physics, problem solving is an essential object of learning. The objective of this research was to propose a system of activities in the Physics course for the Chemical Engineering career that contributes to the students' performance in problem solving by promoting the development of analysis through synthesis. The research assumed the qualitative research paradigm, by means of a pedagogical action research method and a didactic intervention through a system of activities. The systematization of different approaches in the treatment of the subject and the valuation of the role of analysis through synthesis as the basic nucleus of thinking served as the basis for the design of the proposal, which was validated after its implementation through a pretest-posttest strategy. It is concluded that the level of analysis through synthesis in students can be improved with intentional interventions for such purposes.
Keywords: Problem solving; analysis through synthesis; teaching physics; Indicators of analysis development through synthesis.
Resumo
No ensino de Física, a resolução de problemas é um objeto essencial de aprendizagem. O objetivo desta investigação foi propor um sistema de actividades na disciplina de Física do curso de Engenharia Química que contribuísse para o desempenho dos alunos na resolução de problemas, promovendo o desenvolvimento da análise através da síntese. A investigação assumiu o paradigma da investigação qualitativa, recorrendo a um método de investigação-ação pedagógica e a uma intervenção didática através de um sistema de actividades. A sistematização de diferentes abordagens no tratamento do tema e a avaliação do papel da análise através da síntese como núcleo básico do pensamento serviram de base ao desenho da proposta, que foi validada após a sua implementação através de uma estratégia de pré-teste-pós-teste. Conclui-se que o nível de análise através da síntese nos alunos pode ser melhorado com intervenções intencionais para esse efeito.
Palavras-chave: Resolução de problemas; análise através da síntese; ensino da Física; indicadores de desenvolvimento da análise através da síntese.
Introducción
La resolución de problemas constituye un poderoso método para enseñar y aprender ciencias en la escuela (Carrascosa et al., 2020; Lozada & Caballero, 2020), por esta razón, a su estudio se han dedicado muchos investigadores de diferentes enfoques teóricos y de distintas ramas del conocimiento. En particular resultan de interés para este trabajo los estudios realizados por Gil et al. (1992) y continuadores (Valera, 2002; Fernández et al., 2018; Sánchez, 2018; Montero y Mahecha, 2020; Mora et al., 2021) y los de la Facultad de Matemática, Astronomía y Física de la Universidad Nacional de Córdoba: Gangoso & Buteler, (2003); Coleoni & Buteler (2008); Truyol (2012), los cuales se centran en habilidades, características o capacidades que se aspiran a lograr en los estudiantes. Sin embargo, el camino seguido en dichos estudios, aunque aborda el análisis de los procesos mentales o internos, no tiene en cuenta los procesos elementales del pensamiento y sus leyes psicológicas, propuestas por Rubinstein en el contexto del enfoque histórico cultural y que, a juicio de los autores del presente artículo constituyen la base sobre la cual se erigen los procesos internos mencionados.
Se ha hecho mucho énfasis en la importancia de tener en cuenta, las ideas o concepciones previas de los estudiantes para el proceso de enseñanza (Rodríguez, 2018; Meneses, 2019; García, 2020; Rodríguez et al., 2021; Hernández del Barco et al., 2022), pero de igual forma es importante además, tener presente el nivel de desarrollo de los procesos de análisis y síntesis, pues subyacen en el resto de los procesos de pensamiento que aunque son espontáneos su nivel puede no ser el adecuado.
Los estudios de Gil y continuadores intentan romper con la didáctica tradicional de la enseñanza de la resolución de problemas y aproximan esta actividad a la de los investigadores al resolver problemas.
Por otro lado, los investigadores de la Facultad de Matemática, Astronomía y Física de la Universidad de Córdoba, desarrollan una propuesta de resolución de problemas como proceso de modelado, que se concreta en el modelo para la comprensión de problemas de física en los conceptos de Modelo de la Situación, Modelo Físico Conceptual y Modelo Físico Formalizado (Truyol, 2012).
Durante varios años un grupo de investigadores bajo la dirección del psicólogo Rubinstein, realizó un conjunto de investigaciones relativas al pensamiento y la resolución de problemas publicadas en los años 1966 y 1979, relevantes para la comprensión de los procesos mentales implicados en el proceso de resolución de problemas que han sido poco reconocidas en el ámbito académico.
En dichas investigaciones la resolución de problemas se ha usado para poner de manifiesto regularidades psicológicas del pensamiento, que se relacionan con los procesos básicos del pensar, el análisis, la síntesis, la abstracción y la generalización, pero que, por la relación que guardan con el proceso de resolución de problemas, permiten describirlo y emplearlo en su enseñanza y aprendizaje.
Por otro lado, los procesos básicos del pensamiento, según esta teoría psicológica, constituyen la base para el uso de los modelos propuestos por los investigadores de la Universidad de Córdoba, para la compresión de los problemas, así como para el proceso de análisis cualitativo de diferentes situaciones, la emisión de hipótesis y deducción de consecuencias para su comprobación, propuesto por Gil y sus continuadores.
Según Rubinstein el mecanismo básico del pensar es el análisis a través de la síntesis y puede representarse de forma general, mediante un esquema que consiste en “relacionar sus términos con lo que en él se pide y analizar lo uno y lo otro a través de sus reciprocas relaciones.” (Rubinstein, 1979, p. 91)
El análisis a través de la síntesis se ha definido en los siguientes términos:
en el proceso del pensar el objeto entra incesantemente en nuevas relaciones, en virtud de lo cual va adquiriendo nuevas cualidades; de esta suerte parece como si del objeto se fueran sacando nuevos contenidos; es como si este se volviera de lado y presentara nuevas cualidades, que se fijan en nuevas características conceptuales. (Rubinstein, 1979, p. 98)
Reformular significa darle una nueva forma a algo expresado, al sustituirlo por una expresión equivalente, pero que aporta una perspectiva que le ofrece mejores posibilidades para su uso en otro o el mismo contexto. Según Rubinstein (1979) la reformulación en el contexto de la resolución de problemas es expresión del análisis a través de la síntesis, porque en ella subyace el análisis que descubre la dependencia de una proposición respecto a otra, lo que posibilita la sustitución de una por la otra.
Desde este referente teórico el proceso de resolución de problemas consiste en tomar reiteradamente las consecuencias de las condiciones del problema como nueva condición del mismo y la condición más próxima de lo que se pide, como nuevo término desconocido y buscado, repitiéndose estos cambios hasta que la consecuencia más lejana de las condiciones del problema, llegue a unirse con la condición más próxima de lo que se pide (Rubinstein, 1979).
Lo explicado constituye la expresión de la dinámica mental interna del proceso de resolución de problemas, el cual antecede a cualquier intento de análisis cualitativo en la elaboración de los modelos para la comprensión de los problemas, en el caso del proceso de modelado para su resolución.
El análisis y la síntesis, aunque en determinados casos resultan insuficientemente desarrollados para la resolución exitosa de problemas, poseen carácter universal debido a su base neurofisiológica y a su uso en cualquier actividad que requiera del pensamiento (Wertheim y Ragni, 2020), siendo esta la razón que nos conduce a pensar en la necesidad de prestarle la debida atención para lograr su desarrollo.
Metodología y métodos
Se planteó una metodología a partir de un paradigma de investigación cualitativo, mediante un método de investigación acción pedagógica y un conjunto de actividades didácticas. La acción pedagógica estuvo encaminada a desarrollar el análisis a través de la síntesis como mecanismo básico para la resolución de problemas, que propicie, además, una estructura cognitiva favorecedora al aprendizaje de la resolución de problemas. El conjunto de actividades fue planificado con objetivos de aprendizaje propios de contenido, además de otros que respondían al desarrollo paulatino del análisis a través de la síntesis. En su estructuración estas actividades resultaron organizadas como un sistema (González et al., 2021).
En el diseño de las actividades se tuvo en cuenta que, en la resolución de problemas, el análisis a través de la síntesis se expresa en el cambio de las características conceptuales de los objetos del problema, que se manifiestan, en este caso, a través de las magnitudes físicas y las condiciones presentes en él, así como en la reformulación del problema, de sus términos y de lo que en él se pide; por tanto, resulta necesario en cada caso identificar en una situación base y consecuencia.
La propuesta fue implementada en un grupo de estudiantes de primer año de la Carrera de Ingeniería Química de la Universidad de Matanzas, este grupo estuvo formado por 33 estudiantes que participaron por propia voluntad después de conocer las características del estudio y la importancia que tenía para su preparación como ingenieros.
La estrategia utilizada para medir la efectividad de la implementación de la propuesta fue la de realizar pretest y postest, en correspondencia con un diseño no experimental de tipo longitudinal y de carácter cualitativo, para contrastar el nivel de desarrollo inicial con el final y determinar el avance de los estudiantes. Los test empleados al inicio y al final permitieron determinar el nivel de desarrollo del análisis a través de la síntesis.
En la tabla 1 se registran los indicadores utilizados para el análisis a través de la síntesis, además de los criterios para su evaluación. En la tabla 2 se especifica el descriptor de los tres niveles de desarrollo del análisis a través de la síntesis.
Tabla 1. Indicadores del análisis a través de la síntesis y sus criterios de medida
Indicadores |
B |
R |
M |
I1. Reformulación de los términos del problema |
Todas las necesarias |
Algunas de las necesarias |
Ninguna |
I2. Reformulación de la pregunta del problema |
Todas las necesarias |
Algunas de las necesarias |
Ninguna |
I3. Cambio de las características conceptuales de los objetos del problema |
Todos los necesarios |
Algunas de las necesarias |
Ninguno |
Tabla 2. Tabla de niveles del análisis a través de la síntesis
Nivel de desarrollo |
Descriptor |
Alto |
Si tiene B en I1 e I2 y al menos R en I3 |
Medio |
Si tiene B en I1 y R en alguna de las otras |
Bajo |
El resto de los casos |
A continuación, se enuncian los problemas utilizados en el pretest (1) y en el postest (2):
Problema 1. De un punto A de una carretera recta parte un automóvil con velocidad igual a 40 Km/h hacia el punto B que está a 200 Km de A. Si al mismo tiempo partió de B hacia A otro automóvil a 60 Km/h, ¿a qué distancia de A se encontrarán?
Problema 2. La distancia entre el primero y el quinto máximo de un patrón de interferencia es de 0,35 mm. Si la pantalla donde se obtiene el patrón se halla a 413 mm de la doble ranura y la longitud de onda de la luz usada es de 546 nm ¿cuál es la distancia entre las ranuras?
El sistema de actividades fue organizado en seis talleres como actividades prácticas en la asignatura de Física General, en los contenidos de Mecánica, Electromagnetismo y Óptica Física, en la carrera de Ingeniería Química de la Facultad de Ciencias Técnicas de la Universidad de Matanzas, Cuba. En la tabla 3 se exponen los objetivos de estos talleres.
Tabla 3. Objetivo de los talleres del sistema de actividades
Taller |
Objetivo |
I |
Comprender en qué consisten y cómo se producen las reformulaciones de los términos, la pregunta y los problemas, así como los cambios de las características conceptuales de los objetos. |
II |
Identificar las transformaciones explicadas al resolver problemas o valorar la resolución de problemas que otros han resuelto |
III |
Resolver problemas que se resuelven con sistemas de dos ecuaciones con dos incógnitas |
IV |
Resolver problemas con sistemas de tres o cuatro ecuaciones. |
V |
Buscar varias vías de resolución de un problema |
VI |
Abordar la resolución de los problemas desde la concepción de los procesos de modelado |
Acciones a ejecutar por el estudiante en su estudio independiente:
Para medir el nivel de desarrollo del análisis a través de la síntesis, se utilizaron los indicadores definidos en la tabla 1, a manera de ejemplo se expone una variante de resolución del problema 1, donde su análisis se realiza a través de los indicadores definidos.
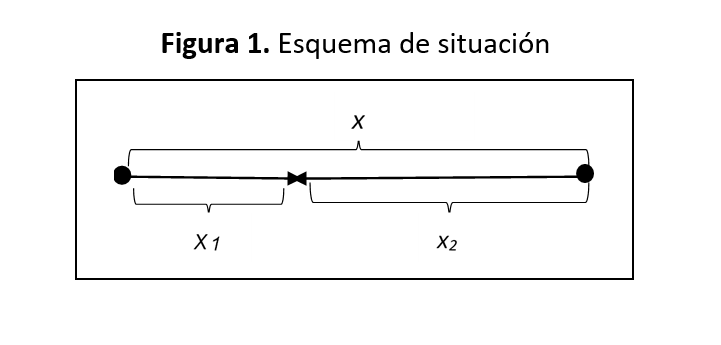
El estudiante conoce que la ecuación de movimiento de un móvil animado de movimiento rectilíneo uniforme es , donde s es la distancia recorrida por el móvil y t es el tiempo que emplea en recorrerla. Al leer el problema actualiza este conocimiento y como lo que se pide es la distancia respecto al punto de partida del primero, puede concluir que: y . En el problema el tiempo es desconocido, pero se dice que parten simultáneamente, luego esta condición del problema puede reformularla planteando que el tiempo que emplea el primero hasta el encuentro, es el mismo que emplea el segundo, o sea, que . Por otro lado, analizando el problema puede construir, como ayuda, un esquema como el que se ilustra en la figura 1.
Figura 1. Esquema de situación

Como se pide a qué distancia del punto de partida del primero se encuentran ambos móviles, se puede reformular esta exigencia a partir de reconocer que , tomando a partir de aquí la condición más próxima de la determinación de x1 que es t1, como nuevo término desconocido y buscado, por lo que de la pregunta ¿cómo hallar s1, se pasa a la pregunta, ¿cómo hallar t1? Como t1 = t2 se pasa a la pregunta cómo hallar t2 y siendo , se repite de nuevo la reformulación con .
Estas reformulaciones se pueden ir integrando como sigue:
A partir de aquí ya no quedan más sustituciones por hacer, solo operar algebraicamente.
Esta misma solución puede ser más breve si se dispone de una estrategia como la siguiente: Si en el problema se relacionan varios móviles se debe plantear una ecuación de movimiento para cada uno. En tal caso deberá encontrar una o más condiciones de ligadura. El estudiante tendrá la posibilidad de disponer al inicio de un modelo matemático para determinar una vía de solución y podrá entonces proceder de la siguiente manera:
Sustituyendo (4) en (1) y (2) y luego (1) y (2) en (3) y (4), se tiene:
y
Debe observarse que, en el proceso de análisis a través de la síntesis, lo que aparece como una simple distancia recorrida por un móvil, resulta también ser un fragmento de la longitud de una pista, con lo cual se ha cambiado la característica conceptual con la que aparece la distancia en la ecuación de movimiento, estos cambios, que se expresan en reformulaciones, pueden suceder continuamente en el proceso de resolución.
En la figura 2 se aprecia como razonó uno de los cuatro estudiantes que resolvió exitosamente el problema del pretest.
Figura 2. Solución de un estudiante en pretest
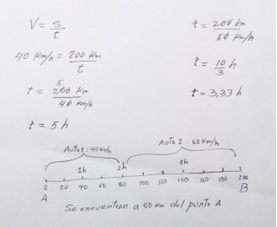
Puede reconstruirse el posible razonamiento de este estudiante del siguiente modo:
Con una velocidad de 40 Km/h el auto 1 emplearía un tiempo de 5h en recorrer los 200Km y el auto 2, 3,3h. Como la velocidad es constante, en una hora el auto 1 recorrería 40Km y el 2, 60Km que sumados serían solo 100Km. Les faltarían otros 100Km más, en los que se encontrarían cuando los tiempos son iguales y el punto de encuentro sería 200 – 60t. Esos razonamientos quedan reflejados en el esquema realizado al final y no al principio del proceso de resolución.
Para valorar el resultado de postest presentamos el caso de un estudiante que no pudo resolver el problema del pretest. En la figura 3 puede observarse la ausencia de reformulaciones y cambios de características conceptuales necesarios para la resolución correcta desde el punto de vista del análisis a través de la síntesis.
Figura 3. Solución de un estudiante en pretest
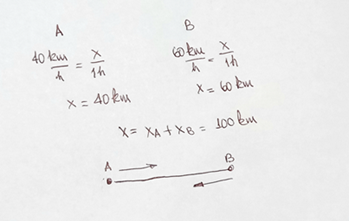
En la figura 4 se muestra lo realizado por este estudiante en el problema del postest, donde se aprecia en el primer esquema dibujado el cambio del enunciado de una forma verbal a una forma gráfica de representación externa, lo que indica su reformulación e incluye en ella la de los términos del problema. Luego, en una representación posterior, se puede observar la reformulación del término distancia del primero al quinto máximo, pero ella está precedida por un cambio de características conceptuales: la distancia del primero al quinto máximo es un segmento de la distancia del central al quinto, que el estudiante llama x2, por lo que x2 = x1 + 0,35 mm. Si el estudiante hubiera denotado de forma diferente la distancia al centro de estos máximos, como x1 y x5, entonces la resolución podría haber continuado de otra forma, como plantaron otros estudiantes, partiendo de que x5 – x1 = 0,35 mm y despejando en las ecuaciones de los máximos x5 y x1 para para sustituirlas en la expresión anterior.
Figura 4. Solución de un estudiante en postest
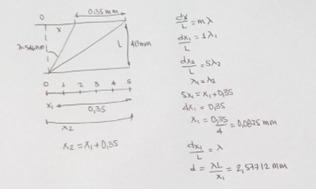
Finalmente, las ecuaciones que expresan las condiciones para los máximos primero y quinto, gracias a la reformulación de la pregunta según la cual, se pasa de buscar cuál es la distancia entre las ranuras, a buscar el valor de la distancia x1 entre el máximo primero y el central, permiten calcularla.
Otro estudiante que tiene en cuenta que en la interferencia las distancias entre los máximos contiguos son iguales, divide la distancia entre el primer y el quinto máximo entre cuatro y determina el valor de la distancia entre dos contiguos cualesquiera, la cual es a su vez, igual a la distancia del central al primero y tomando esta distancia como x1 calcula la distancia entre las dos ranuras.
Aun cuando se observa la ausencia de una experiencia que muestre el dominio de estrategias elaboradas para el enfrentamiento del problema, puede apreciarse la realización del análisis a través de la síntesis, por la presencia de las reformulaciones y cambios de características conceptuales que, aunque no concientizadas, son realizadas porque resultan ineludibles al resolver el problema.
Tabla 4. Resultados de los Indicadores del análisis a través de la síntesis en pretest
Indicadores |
B |
R |
M |
I1. Reformulación de los términos del problema |
5 (15.2 %) |
0 (0.0 %) |
28 (84.8 %) |
I2. Reformulación de la pregunta del problema |
4 (12.1%) |
0 (0.0 %) |
29 (87.9 %) |
I3. Cambio de las características conceptuales de los objetos del problema |
4 (12.1%) |
0 (0.0 %) |
29 (87.9 %) |
El nivel bajo de desarrollo del análisis a través de la síntesis con que los estudiantes son evaluados al comenzar el curso son evidencia de que llegan a la universidad con un deficiente desarrollo de estos procesos, lo cual atenta contra el éxito en la resolución de problemas. Este resultado se alinea con el estudio desarrollado por Poveda (2022), que aunque no trabaja específicamente el análisis a través de la síntesis si refiere otras habilidades cognitivas implicadas en la resolución de problemas en Física y su incidencia en el éxito de este proceso.
El sistema de actividades propuesto fue diseñado para potenciar el desarrollo de las habilidades de pensamiento que propician el análisis a través de las síntesis y con ello favorecer al aprendizaje de la resolución de problemas. Los resultados de la aplicación del instrumento de evaluación posterior a la intervención se muestran en la tabla 5. En ella se evidencia como los estudiantes logran mejorar los indicadores que evalúan el nivel del análisis a través de la síntesis. Puede apreciarse como los indicadores I1 e I3 mejoran considerablemente, el I2 aunque mejora solo el 63.4% de los estudiantes son evaluados de Bien.
Tabla 5. Resultados de los Indicadores del análisis a través de la síntesis
Indicadores |
B |
R |
M |
I1. Reformulación de los términos del problema |
27 (81.8%) |
1 (3.0 %) |
5 (15.2 %) |
I2. Reformulación de la pregunta del problema |
12 (36.4%) |
14 (42.4%) |
7 (21.2 %) |
I3. Cambio de las características conceptuales de los objetos del problema |
25 (75.8%) |
1 (3.0 %) |
7 (21.2 %) |
En la tabla 6 se muestra la cantidad de estudiantes en cada nivel de desarrollo del análisis a través de la síntesis antes y después de la intervención. Como puede verse el número de estudiantes evaluados en un nivel al menos Medio aumenta con la intervención.
Tabla 6. Nivel de desarrollo del Análisis a través de la síntesis antes y después de la intervención
|
Nivel de desarrollo del análisis a través de la síntesis Postest |
Total |
|||
Bajo |
Medio |
Alto |
|||
Nivel de desarrollo del análisis a través de la síntesis Pretest |
Bajo |
7 |
14 |
8 |
29 |
Alto |
0 |
0 |
4 |
4 |
|
Total |
7 |
14 |
12 |
33 |
|
Para corroborar que esa diferencia es estadísticamente significativa, se aplicó la prueba estadística inferencial no paramétrica de rangos con signo de Wilcoxon (Ortega et al., 2021), se utilizó el SPSS 20 para tal propósito, se obtuvo un p-valor de 0.0, lo que permitió afirmar que el nivel medio de desarrollo del análisis a través de la síntesis es mayor después de la intervención con el sistema de actividades.
Los resultados presentados permiten apreciar un incremento en el número de estudiantes que elevaron su nivel de desarrollo del análisis a través de la síntesis, quedando solo un pequeño grupo sin lograrlo. Esto da muestra de la efectividad de la propuesta realizada a través del sistema de actividades como con una intervención intencionada a potenciar el desarrollo del análisis a través de la síntesis.
Desde su concepción se consideraron las sugerencias de Espinosa (2021) de complementar el aprendizaje disciplinar, en este caso de la Física, con el desarrollo de habilidades cognitivas. En su diseño se tuvo en cuenta los aportes de Truyol, (2012), al considerar las potencialidades que tienen las acciones que desarrollan los estudiantes para realizar las representaciones mentales y establecer sus relaciones como marcadores para clasificar a los estudiantes como expertos y novatos (Álvarez et al., 2020).
En estos resultados, que los autores consideran positivos, influyeron tanto factores que contribuyeron a su logro como factores adversos, estando entre los primeros la propia estrategia implementada la cual se basó en los resultados de importantes investigaciones realizadas. Entre los factores del segundo tipo se encuentran, además del insuficiente nivel inicial de desarrollo cognitivo de los estudiantes, así como de dominio de los conocimientos de física, el hecho de que la estrategia exigía un esfuerzo individual que, por lo dilatado del tiempo que duro el trabajo desarrollado, fue difícil de mantener en algunos casos.
En el estudio realizado se aprecian reformulaciones y cambios conceptuales, al valorar las soluciones desde los modelos mencionados, con lo cual se evidencia su presencia en el proceso real de la resolución de problemas. Se observa además que a una correcta solución de un problema solo puede llegarse, si se realizan correctamente las reformulaciones y cambios de las características conceptuales que caracterizan al análisis a través de la síntesis.
Conclusiones
A modo de conclusión se puede afirmar que el análisis a través de la síntesis como núcleo básico del pensar, por su naturaleza universal y espontánea, está presente en toda la actividad mental que el sujeto realiza para interpretar, comprender y resolver las situaciones que se le presentan en la vida, entre ellas la resolución de problemas sean o no de tipo académicos.
En el presente trabajo se defiende la idea de que los modelos de la resolución de problemas como investigación y como proceso de modelado, con los que se intenta comprender cómo se produce la resolución de problemas y cómo conducir su enseñanza, deben ser completados con la incorporación del análisis a través de la síntesis.
Con la incorporación del análisis a través de la síntesis a estrategias para la enseñanza de la resolución de problemas, se puede lograr una toma de conciencia que favorece la metacognición, en relación con los procesos más elementales del pensar que, de otra forma, escapan al control de la enseñanza.
Referencias bibliográficas
Álvarez, V., Torres, T., Gangoso, Z., & Sanjosé, V. (2020). A Cognitive Model to Analyse Physics and Chemistry Problem-Solving Skills: Mental Representations Implied in Solving Actions. Journal of Baltic Science Education, 19(5), 730-746. https://files.eric.ed.gov/fulltext/EJ1270831.pdf
Carrascosa, J., Martínez, S., & Alonso, M. (2020). Competencia Científica y Resolución de Problemas de Física. Revista científica, (38), 201-215. https://doi.org/10.14483/23448350.16211.
Coleoni, E., & Buteler, L. (2008). Recursos metacognitivos durante la resolución de un problema de Física. Investigações em Ensino de Ciências, 13(3), 371-383. https://ienci.if.ufrgs.br/index.php/ienci/article/view/447.
Espinosa, L. (2021). Pensamiento metacognitivo, crítico y creativo en contextos educativos: conceptualización y sugerencias didácticas. Psicologia Escolar e Educacional, 25. https://www.scielo.br/j/pee/a/TyBjd8mLtVxRC8Dr64bSmMk/?lang=es
Fernández, J., Carrillo, J. & Conde, S. (2018). Un estudio de caso para analizar cómo ayudan los profesores en resolución de problemas matemáticos. Educación Matemática, 30(3). http://doi.org/10.24844/EM3003.10
Gangoso, Z., & Buteler, L. (2003). La representación externa en la resolución de un problema de Física: ¿una cuestión de forma o una cuestión de fondo? Cognitiva, 15(1), 51-66. https://www.researchgate.net/profile/Laura-Buteler/publication/39208328
García, C.E. (2020). Formación para el análisis, el pensamiento crítico y la solución de problemas en las universidades regionales. Revista Guillermo de Ockham, 18(2), 127-136. http://www.scielo.org.co/scielo.php?pid=S1794-192X2020000200127&script=sci_arttext
Gil, D., Martínez, J., Ramírez, L., Dumas, A., Gofard, M., & Pessoa de Carvalho, A.M. (1992). La didáctica de la resolución de problemas en cuestión: elaboración de un modelo alternativo. Didáctica de las ciencias experimentales y sociales, 6, 73-85. http://hdl.handle.net/11162/22307.
González, E., Ríos, L.R & Hernández, Y. (2021). Validación científica de un sistema de actividades didácticas sustentado en un aula virtual para desarrollar la competencia fonológica en francés. Opuntia Bravas, 13 (1), 175-189. https://hal.science/hal-03584624.
Hernández del Barco, MA., Cañada, F., Cordovilla, AM. & Airado, D. (2022). An approach to epistemic emotions in physics’ teaching-learning. The case of pre-service teachers, Heliyon, 8(11). https://doi.org/10.1016/j.heliyon.2022.e11444
Lozada, J.A.D., & Caballero, J.R.D. (2020). La resolución de problemas desde un enfoque epistemológico. Foro de educación, 18(2), 191-209. http://dx.doi.org/10.14516/fde.694
Meneses, M.L. (2019). Método de Polya como estrategia para fortalecer la competencia resolución de problemas matemáticos con operaciones básicas. Zona Próxima, 31, 7-25. https://doi.org/10.14482/zp.31.372.7.
Montero, L. & Mahecha, J. (2020). Comprensión y resolución de problemas matemáticos desde la macroestructura del texto. Praxis & Saber, 11(26), e9862. https://doi.org/10.19053/22160159.v11.n26.2020.9862.
Mora, F.B., Rodríguez, A.R., Nava, M.C., & Álvarez, C.R. (2021). Resolución de problemas en el aprendizaje y enseñanza de las matemáticas. Pädi Boletín Científico de Ciencias Básicas e Ingenierías del ICBI, 9 (Especial), 10-17. https://doi.org/10.29057/icbi.v9iEspecial.7051
Ortega, E., Ochoa, C. & Molina M. (2021). Pruebas no paramétricas. Evid Pediatr, 17(3). https://evidenciasenpediatria.es/articulo/7892/pruebas-no-parametricas.
Poveda, I.L. (2022). Incidencia del uso de habilidades de pensamiento metacognitivo en la solución de problemas: Caso estudiantes de física mecánica para ingeniería en Bogotá, Colombia. Investigações em Ensino de Ciências, 27(2), 57-77. https://doi.org/10.22600/1518-8795.ienci2022v27n2p57
Rodríguez, L.E. (2018). Evaluación de cualidades del pensamiento de estudiantes de Matemática-Física al ingreso a la universidad. Revista Actualidades Investigativas en Educación, 18 (2), 1-23. http://dx.doi.org/10.15517/aie.v18i2.33036
Rodríguez, L.E., Pérez, Y. & Pérez, N.P. (2021). La habilidad para formular problemas en la enseñanza y el aprendizaje de la solución de problemas de Física y de Matemática. Luz, 20 (1), 40-54. https://luz.uho.edu.cu/index.php/luz/article/view/1081
Sánchez, S. (2018). Programa Eureka en la resolución de problemas matemáticos en estudiantes de tercer grado de primaria. Revista Educación y Desarrollo Social, 12(2), 5-14. https://doi.org/10.18359/reds.4356.
Truyol, M.L. (2012). Comprensión y Modelado en la Resolución de Problemas en Física. Un estudio en Nivel Superior. Tesis doctoral. Universidad Nacional de Córdoba. https://www.famaf.unc.edu.ar/documents/1053/DFis163.pdf.
Wertheim, J. & Ragni, M. (2020). The Neurocognitive Correlates of Human Reasoning: A Meta-analysis of Conditional and Syllogistic Inferences. J Cogn Neurosci, 32 (6): 1061–1078. https://doi.org/10.1162/jocn_a_01531
Contribución autoral:
Maritza Petersson Roldán: conceptualización, curación de datos, análisis formal, revisión, edición y envió del trabajo.
Arnaldo Vicente Morey Ramos: conceptualización, investigación, determinación y descripción de la metodología, redacción del borrador original.
Declaración de conflictos de interés:
Loa autores declaran que no existen conflicto de intereses.
Atenas Nro. 62 (2024) ISSN: 1682-2749
https://atenas.umcc.cu